트리의 개념
트리(tree)는 계층적인 자료를 표현하는데 적합한 자료구조이다.
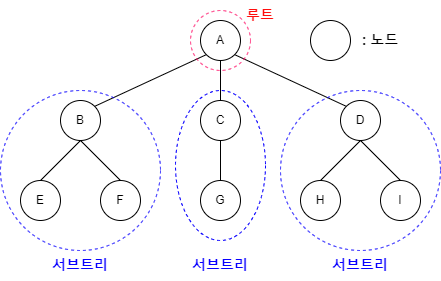
트리의 구성 요소에 해당하는 A, B, C, D, E, F, G, H, I, J를 노드(Node)라 한다.
트리는 한 개이상의 노드로 이루어진 유한 집합이다. 이들 중 하나의 노드는 루트(root) 노드라 불리고 나머지 노드들은 서브 트리(subtree)라고 불린다. 계층적인 구조에서 가장 높은 곳에 있는 노드인 A가 루트가 된다. 위 노드에서 루트 노드는 A이고, 나머지 노드들은 {B, E, F}, {C, G}, {D, H, I}로 3개의 집합으로 나누어지는데 이들을 A의 서브트리라고 한다. 다시 서브 트리인 {B, E, F}의 루트는 B가 되고 나머지 노드들은 다시 2개의 서브 트리, 즉 {E}, {F}로 나누어진다.
트리에서 루트와 서브트리는 선으로 연결된다. 이 연결선을 간선(edge)라고 한다. 노드들 간에는 부모 관계, 형제 관계, 조상과 자손 관계가 존재한다. 이들은 모두 인간의 관계와 동일하다. 즉, 위 그림에서 A는 B의 부모 노드(parent node)가 된다. 반대로 B는 A의 자식 노드(children node)가 된다. B와 C와 D는 형제 관계(sibling)이다.

노드의 차수(degree)는 어떤 노드가 가지고 있는 자식 노드의 개수를 의미한다. 위 그림에서 루트 노드의 경우, 자식 노드가 3개이기 때문에 차수도 3이 된다. 트리의 차수는 트리가 가지고 있는 노드의 차수 중에서 가장 큰 값이다. 위 그림은 A 노드의 차수가 3으로 가장 크므로 전체 트리의 차수가 3이 된다.
트리의 종류

트리를 컴퓨터 메모리상에서 표현하는 방법은 여러 가지가 있을 수 있다. 트리를 프로그램 안에서 표현하는 가장 일반적인 방법은 위 그림과 같다. 각 노드가 데이터를 저장하는 데이터 필드와 자식 노드를 가리키는 링크 필드를 가지게 하는 것이다. n은 자식 노드의 개수, 즉 노드의 차수이다. 일반적인 트리에서 각 노드들을 서로 다른 개수의 자식 노드를 가지므로 노드에 따라서 링크 필드의 개수가 달라진다.

이 방법의 문제점은 노드의 크기가 고정되지 않는다는 것이다. 즉 노드에 붙어 있는 자식 노드의 개수에 따라서 노드의 크기가 커지기도 하고 작아지기도 한다. 이와 같이 노드의 크기가 일정하지 않으면 프로그램이 복잡하게 된다. 위 그림처럼 이진 트리를 사용하면 이런 문제점을 해결할 수 있다. (사실 일반 트리도 이진 트리로 변환할 수 있는 방법이 존재한다.)
이진 트리의 정의
트리 중에서 가장 많이 쓰이는 트리가 이진트리이다. 모든 노드가 2개의 서브 트리를 가지고 있는 트리를 이진 트리(binary tree)라고 한다. 서브 트리는 공집합일 수 있다. 따라서 이진트리의 노드에는 최대 2개까지의 자식 노드가 존재할 수 있고 모든 노드의 차수가 2 이하가 된다. 공집합도 이진 트리라는 점에 주의해야 한다. 또한 이진 트리에는 서브 트리간의 순서가 존재한다. 따라서 왼쪽 서브 트리와 오른쪽 서브 트리는 서로 구별된다.
이진트리는 다음과 같이 정의된다.
(1) 공집합이거나
(2) 루트와 왼쪽 서브 트리, 오른쪽 서브 트리로 구성된 노드들의 유한 집합으로 정의된다. 이진트리의 서브트리들은 모두 이진트리여야 한다.

이진트리의 성질
1. n개의 노드를 가진 이진트리는 정확하게 n-1의 간선을 가진다.
2. 높이가 a인 이진트리의 경우, 최소 a개의 노드를 가지며 최대 2ª-1개의 노드를 가진다.
3. n개의 노드를 가지는 이진트리의 높이는 최대 n이거나 최소 ⌈log₂(n+1)⌉이 된다. 그 이유는 레벨 당 최소한 하나의 노드는 있어야 하므로 높이가 n을 넘을 수는 없다. 그리고 앞의 성질에서 높이 h의 이진트리가 가질 수 있는 노드의 최대값은 2ª-1이다. 따라서 n ≤ 2ª-1의 부등식이 성립하고 양변에 log를 취하여 정리하면 a ≥ log₂(n+1)이 된다. a는 정수이어야 하므로 a ≥ ⌈log₂(n+1)⌉이 된다. ⌈...⌉은 올림 연산으로 ⌈2.4⌉는 3이 된다.
참고
- C언어로 쉽게 풀어쓴 자료구조 책
'자료구조 알고리즘 > 공부' 카테고리의 다른 글
| [자료구조] 덱 (0) | 2022.04.03 |
|---|---|
| [자료구조] 큐 (0) | 2022.04.03 |
| [자료구조] 스택을 이용해 미로 탐색하기 (0) | 2022.03.29 |
| [자료구조] 스택 (0) | 2022.03.18 |
| [자료구조] 배열 (0) | 2022.01.30 |
![[자료구조] 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FPOBYW%2FbtryDkkC6LW%2FK03bMrdHbK6WQxspZljgGk%2Fimg.png)